Home Page Brainteasers Guess The Photo For Geeks & Brainiacs Lateral Thinking Number Puzzles Perceptual Puzzles Riddles Spot The Difference Target Number Word Puzzles Monthly Puzzle Contest Monthly Contest Winners Monthly Newsletter Link To Us References Send Us Your Puzzle Printable Puzzles Logic Puzzles Solitaire Games

Follow us:

Share this page on:

Need a Hint?

HINT: The best way to tackle this is to use a probability tree diagram. You can find an example here.

See Answer

ANSWER: $55.

EXPLANATION: Either the test is registered correctly (60% probability) or it has been affected by a system glitch (40% probability). If it had been affected by a system glitch, we know that the first digit in his actual score could have been any number from 1 to 9 but the second digit had to have been a 5. So we can make a probability tree diagram to determine Joe's score based on statistical probability:
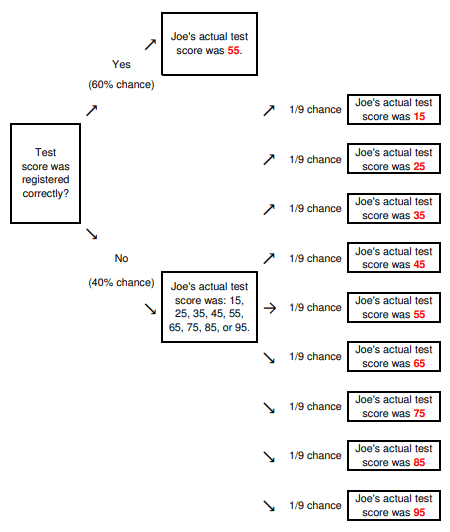
The long way would be to add up the probabilities multiplied by the associated score for each row: (0.6 * 55) + (0.4 * 1/9 * 15) + (0.4 * 1/9 * 25) + (0.4 * 1/9 * 35) + (0.4 * 1/9 * 45) + (0.4 * 1/9 * 55) + (0.4 * 1/9 * 65) + (0.4 * 1/9 * 75) + (0.4 * 1/9 * 85) + (0.4 * 1/9 * 95) = 55.

Or, if you noticed that whether the test was registed correctly or not, in each case the average test score is 55 (and an equal probabilty of all 9 scores if the test score that was not registered correctly), the result will therefore be 55. So, statistically, you would expect to have $55. Note that the percentage of tests that were affected by the glitch is not relevant.

Do you have a suggestion for this puzzle (e.g. something that should be mentioned/clarified in the question or solution, bug, typo, etc.)?

<- Previous puzzle | Next puzzle ->

Click here to return to the list of puzzles

Contact Us| Bookmark Site| Terms Of Use| Privacy Policy